|
Update: using Manhattan distance in k-means
Note the capital 'K' in Kmeans function from the amap package.
Using 'Manhattan distance' puts more weight to sparsely distributed locations. As a result, we can see more proposed EV locations in remote areas and less in downtown.
Code is published on my github.
Previously, I did some analysis on car2go's location data to find the most popular roads in Austin. But we can do much more. One question I have is: if car2go wants to replace the entire Austin fleet with electric vehicles, where should the charging stations be? Can we use the existing public charging stations? How many more shall we build and where? In this article, I will try to answer them using the data I scraped. If ever one day car2go decides to do so, it should be a more thorough analysis than this one, especially in business domain. However, this could be a good starting point.
Fun fact: Car2go has the only all-EV fleet in San Diego in the whole US. Location data
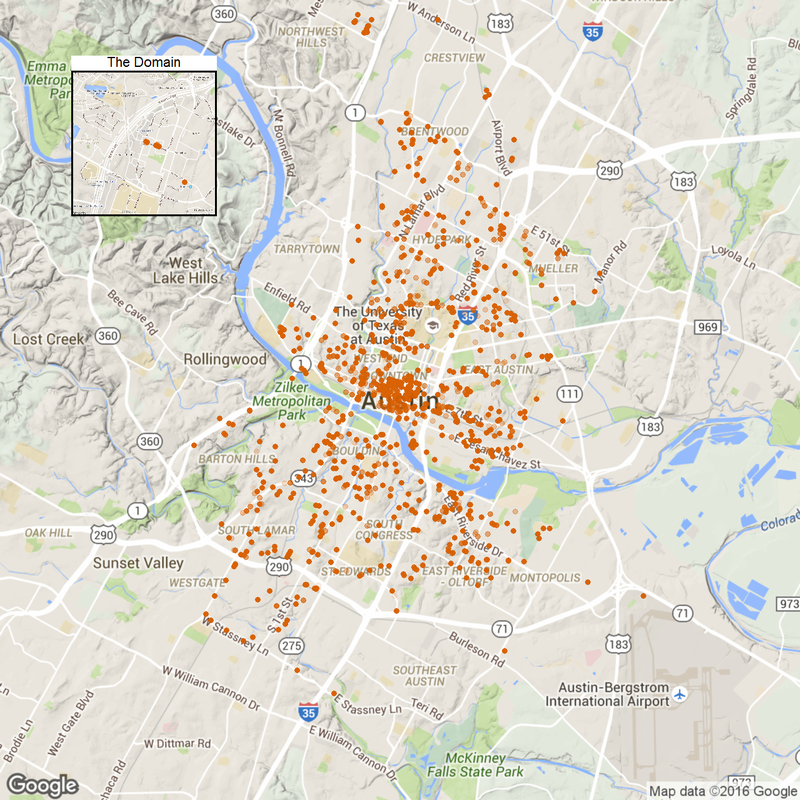
I'll use the locationI scraped last month. A car will have multiple entries because it is not constantly moving. Those duplicated entries seem redundant at first. However, since charging an EV takes substantially more time than filling the tank, a car staying at one place for a prolonged time makes this place more suitable for a charging station. Therefore, these entries puts more weight in my algorithm later on.
First, let's see those locations. library(ggmap) library(grid) library(dplyr) library(ggplot2) library(broom) time.df <- read.csv('data/1Timedcar2go_week.csv', header = T) #car location plot p1<- ggmap(get_map(location = 'austin', zoom = 12), extent = 'device')+ geom_point(aes(x = Longitude, y = Latitude), data = time.df, alpha = 0.1, color = '#D55E00', size = 4) + theme(legend.position = 'none') p1.2<- ggmap(get_map('domain, austin', zoom = 15), extent = 'device')+ geom_point(aes(x = Longitude, y = Latitude), data = time.df, alpha = 0.1, color = '#D55E00', size = 4) + ggtitle('The Domain')+ theme(legend.position = 'none', plot.title = element_text(size = rel(2)), panel.border = element_rect(colour = "black", fill = NA, size=2)) plot_inset <- function(name, p1, p2){ png(name, width=1280, height=1280) grid.newpage() v1<-viewport(width = 1, height = 1, x = 0.5, y = 0.5) #plot area for the main map v2<-viewport(width = 0.2, height = 0.2, x = 0.18, y = 0.83) #plot area for the inset map print(p1,vp=v1) print(p2,vp=v2) dev.off() } plot_inset('1.png', p1, p1.2)
Note those remote home areas: the domain, far west and the parking spot near airport.
Finding optimal location for charging stations
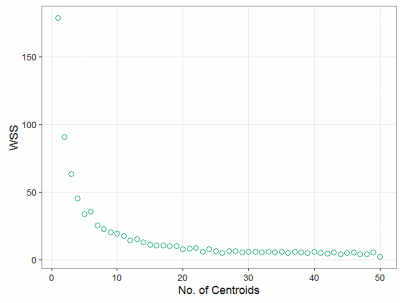
To locate optimal charging stations, we need to minimize the distance that car2go staff have to move the car from where it is returned to the station. One method immediately coming to mind is K-means. It does exactly what we need to find those locations (or centroids). So the next question is: how many charging stations? Can we use the data to determine the number? Let's plot the within-group sum of square.
set.seed(18) wss <- data.frame(clusterNo = seq(1,50), wss = rep(0, 50)) for (i in 1:50){ clust.k <-time.df %>% select(Longitude, Latitude) %>% kmeans(i, iter.max=500) wss$wss[i] <- clust.k$tot.withinss } p2 <- ggplot(wss)+geom_point(aes(clusterNo, wss), size = 4, shape = 1, color='#009E73')+ xlab('No. of Centroids') + ylab('WSS') + theme_bw(18) png('2.png', width=640, height=480) print(p2) dev.off()
So it seems after 10, the overall WSS reduction is not significant wrt increasing no. of centroids. But is this the optimal number? It seems too few. We have to consider more aspects: cost of a new charging station, cost of moving the vehicles per unit distance, max range of a car, or even towing expence. All these requires more data and a business mind. For the sake of this article, I will assume building a charging station is relatively cheap and top priority is customer convenience. So let's take 50 charging stations.
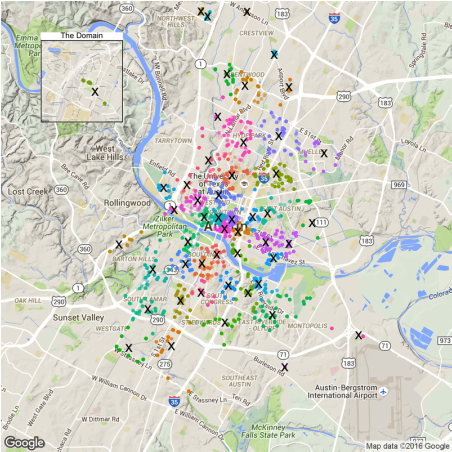
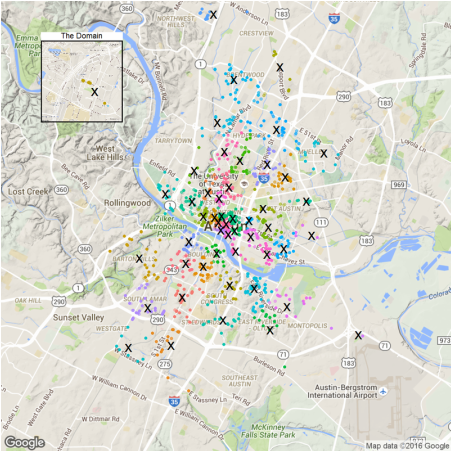
#50 charging station clust <- time.df %>% select(Longitude, Latitude) %>% kmeans(50, iter.max=500) p3<- ggmap(get_map(location = 'austin', zoom = 12), extent = 'device')+ geom_point(data=augment(clust, time.df), aes(x = Longitude, y = Latitude, color = .cluster), alpha =0.1, size = 4) + geom_point(aes(Longitude, Latitude), data = data.frame(clust$centers), size = 15, shape = 'x') + theme(legend.position = 'none') p3.2<- ggmap(get_map('domain, austin', zoom = 15), extent = 'device')+ geom_point(data=augment(clust, time.df), aes(x = Longitude, y = Latitude, color = .cluster), alpha =0.1, size = 4) + geom_point(aes(Longitude, Latitude), data = data.frame(clust$centers), size = 15, shape = 'x') + ggtitle('The Domain')+ theme(legend.position = 'none', plot.title = element_text(size = rel(2)), panel.border = element_rect(colour = "black", fill = NA, size=2)) plot_inset('3.png', p3, p3.2)
So the crosses in the figure are proposed charging stations. The algorithm suggests we deploy the station at each of those remote home areas: the domain, far west and the parking spot near airport. More stations should be deployed in downtown as expected.
Using existing public charging stations
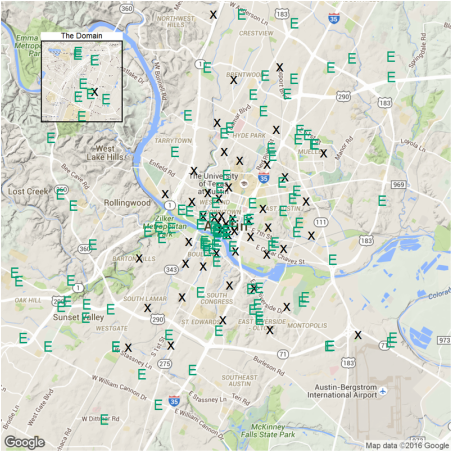
For those locations, can we use existing charging stations in Ausin? I downloaded ev station data from here: http://www.afdc.energy.gov/data_download/. Now let's plot proposed (X) and existing stations (E) together.
station.df <- read.csv('data/charging_stations (Feb 20 2016).csv', header = T) station.austin = station.df%>%dplyr::filter(City=='Austin') p4<- ggmap(get_map(location = 'austin', zoom = 12), extent = 'device')+ geom_point(aes(Longitude, Latitude), data = data.frame(clust$centers), size = 15, shape = 'x') + geom_point(aes(x = Longitude, y = Latitude), data = station.austin, size = 14, shape = 'E', color = '#009E73') + theme(legend.position = 'none') p4.2<- ggmap(get_map('domain, austin', zoom = 15), extent = 'device')+ geom_point(aes(Longitude, Latitude), data = data.frame(clust$centers), size = 15, shape = 'x') + geom_point(aes(x = Longitude, y = Latitude), data = station.austin, size = 14, shape = 'E', color = '#009E73') + ggtitle('The Domain')+ theme(legend.position = 'none', plot.title = element_text(size = rel(2)), panel.border = element_rect(colour = "black", fill = NA, size=2)) plot_inset('4.png', p4, p4.2)
Again, downtown is well covered. But residential areas like Barton hills and South Lamar are not. The reason is that public EV stations are often built in places of interest (e.g. malls) while car2go parking rules require the cars to park on street meters. If I have to park at a mall, I need to pay the entire duration. So given this fact, it is not suprising that additional charging stations are needed.
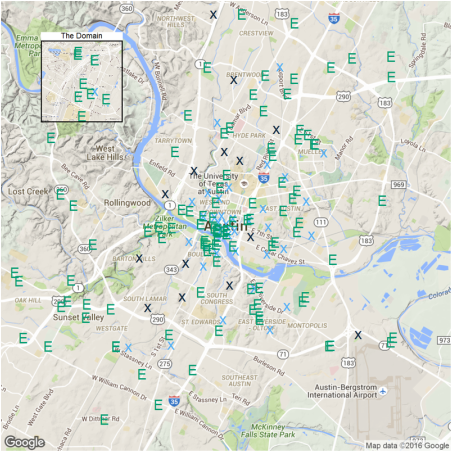
The criteria for a new station is that no existing station is within 0.5 miles of the proposed station. station.dist <- mutate(data.frame(clust$centers), distToExist= 0) for (i in 1:nrow(station.dist)){ # In the area of Austin, one dgree in Latitude is 69.1 miles, # while one degree in Longitude is 59.7 miles d <- sqrt(((station.austin$Latitude-station.dist$Latitude[i])*69.1)**2 +((station.austin$Longitude-station.dist$Longitude[i])*59.7)**2) station.dist$distToExist[i] <- min(d) } p5 <-ggmap(get_map(location = 'austin', zoom = 12), extent = 'device')+ geom_point(aes(Longitude, Latitude, color = -sign(distToExist-0.5)), data = station.dist, size = 15, shape = 'x') + geom_point(aes(x = Longitude, y = Latitude), data = station.austin, size = 14, shape = 'E', color = '#009E73') + theme(legend.position = 'none') p5.2<- ggmap(get_map('domain, austin', zoom = 15), extent = 'device')+ geom_point(aes(Longitude, Latitude, color = -sign(distToExist-0.5)), data = station.dist, size = 15, shape = 'x') + geom_point(aes(x = Longitude, y = Latitude), data = station.austin, size = 14, shape = 'E', color = '#009E73') + ggtitle('The Domain')+ theme(legend.position = 'none', plot.title = element_text(size = rel(2)), panel.border = element_rect(colour = "black", fill = NA, size=2)) plot_inset('5.png', p5, p5.2)
The light-blue crosses represent a station very close to existing ones and dark-blue crosses are new one to be built. There are 14 in total.
Conclusion
OK there you have it. I just used the k-means method to propose new charging stations if car2to decides to deploy an all-EV fleet in Austin. There are 14 locations that require new charging stations. Most of these locations are residential areas far from downtown, where the EV infastructure is lacking.
Back to R script, k-means is really easy to implement. The harder part is to connect the data with business insights.
4 Comments
Interesting read. Nice to see how less code is necessary to obtain those results meanwhile.
Reply
Thanks for your read!
Reply
Long
2/28/2016 06:40:53 pm
Even in k-means, the objective isn't euclidean distance...replacing the objective with sum of distances, e.g. euclidean or manhattan, would make the problem difficult.
Reply
Jun
2/28/2016 07:55:00 pm
Why is that?
Reply
Leave a Reply. |
AuthorA mechanical engineer who also loves data. Archives
January 2018
CategoriesBlogs I enjoy reading |
 RSS Feed
RSS Feed
